Pitagora, oltre ad essere un grande matematico, fu anche cultore della musica. Proprio questa sua passione lo portò a studiare quale rapporto potesse esistere tra i numeri naturali e la musica.
Pare, anche se non vi sono conferme in merito, che fu lui ad inventare uno strumento, il monocordo, che, come il suo stesso nome suggerisce, era costituito da una sola corda, tesa tra due ponticelli sopra una cassa armonica; sotto la corda un terzo ponticello mobile permetteva di dividere la corda stessa a piacere, dando origine a suoni diversi.
Dalle sue prove sul monocordo Pitagora intuì che una corda messa in vibrazione produce un suono la cui altezza percepita dall’orecchio umano è in stretta relazione con la lunghezza della corda stessa.
Ovviamente il filosofo di Samo non poteva avere conoscenza della fisica dei suoni, ovvero del rapporto esistente tra l’altezza di un suono e la frequenza dell’onda sonora associata; solamente si accorse che più la corda è lunga, più la nota prodotta viene avvertita come “bassa” o “grave”; al contrario una corda più corta produce una nota che viene percepita dall’orecchio umano come più “alta” o “acuta”.
Pitagora, essendo un matematico, ebbe l’idea di associare ogni nota ad un numero, ovvero l’inverso della lunghezza della corda che generava un dato suono.
In altre parole, associò al numero 1 la nota prodotta da una corda lunga 1 metro, e al numero 2 la nota prodotta da una corda lunga mezzo metro, e via così.
Con utilizzo dell’inverso della lunghezza le note più acute risultano definite con numeri più grandi, in modo da conciliare l’altezza della nota con il valore del numero che la rappresenta. Ovvero, ogni nota risulta contraddistinta da un numero che è proporzionale alla propria frequenza.
Con successive sperimentazioni Pitagora scoprì che le note sono legate tra di loro da un rapporto numerico semplice, ovvero da un numero razionale, rapporto tra due numeri interi.
Infatti, facendo vibrare una corda che produce la nota definita dal numero 1, e poi quella che genera un suono associato al numero 2, corda di metà lunghezza, otteniamo due suoni che l’orecchio umano, identifica come molto simili, quasi uguali. Questo intervallo è quello che successivamente è stato chiamato “ottava”. Il rapporto è quindi definito da numeri interi: 2:1.
I suoni così generati sono detti “armoniche”.

Pitagora verificò anche che esiste un rapporto 3:2. Tale rapporto può essere visto come = 1,5, quindi prodotto da una corda lunga 2/3 rispetto alla prima.
In questo caso l’orecchio umano non percepisce più le note come simili o quasi uguali, ma piuttosto come suoni legati da armonia e, quindi, particolarmente gradevoli. Il rapporto 3:2 è definito in musica “quinta”.
Successivamente con il rapporto 4:3 si definisce la “quarta”. Tra due suoni di “quarta” è presente un tono di disgiunzione.
Proseguendo si arriva fino alla nota definita dal rapporto 9:8 chiamata “seconda”. Tale tono era considerato da Pitagora quello di base e, in seguito, definito “Tono pitagorico”.
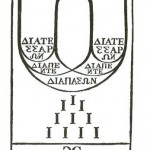
In un celebre affresco, “La scuola di Atene” di Raffaello Sanzio è raffigurato, tra gli altri, un giovane che presenta a Pitagora una tavoletta, chiamata Epogdoon:
Nell’Epogdoon si vede la suddivisione pitagorica dell’ottava, che, come detto in precedenza, prevede due intervalli di quarta separati da un tono detto tono di disgiunzione contrassegnato con il piccolo arco nella parte superiore. Il termine Epogdoon indica, appunto, il rapporto di 9/8 che caratterizza il tono pitagorico. I numeri romani nella parte superiore VI, VIIII VIIII e XII indicano la forma in cui venivano caratterizzate nel pitagorismo, con riferimento al monocordo, l’ottava (6,12), la quinta (6,9 e 8,12), la quarta (6,8 e 9,12) e la fondamentale (12,12).
In basso come variante rispetto ai numeri 1,2,3,4, è posizionata la forma simbolica della Tetraktys.
Riguardo la Tetrakys suggerisco un illuminante scritto di Vincenzo Gueglio, antico collega di scuole, “Pitagora, il Tao e la radice di due” presente nel sito dell’Istituto tecnico di Chiavari.
Cfr. Barbara Münxelhaus, Pythagoras musicus, Bonn 1976, p. 190
«Solo un arco, tra 8 e 9, è tracciato in alto, con la sovrascritta epogdoon. Raffaello impiega qui la designazione greca per il rapporto 9:8,, che corrisponde al tono intero. Il tono intero non viene annoverato tra le consonanze. ma risulta dalla struttura degli intervalli consonanti. Attraverso il tono intero vengono separate le due quarte 6/8 e 9/12 che corrispondono nel sistema tonale greco ai tetracordi meson e diezeugmenon, che sono separati dal tono intero che rappresenta la “diazeugsis” È possibile che alla parola “epogdoon” che vale quasi come titolo della tavola, spetti anche la funzione di fornire un rimando alla tradizione, secondo la quale fu Pitagora ad avere introdotto nella scala il tono intero a 9:8, o almeno a mettere in evidenza l’importanza che questo tono ha per la scala pitagorica».